Regra de Chió (Determinantes de Matrizes de Ordem 4)

Para encontrar determinantes de Matriz 4 x 4, pode-se utilizar a Regra de Chió. 

Antes de adentrarmos propriamente na regra, vamos rever uma característica importantes das matrizes:

"Multiplicando por um número real todos os elementos de uma fila em uma raiz, o determinante dessa matriz fica multiplicado por esse número"

Agora, comecemos:

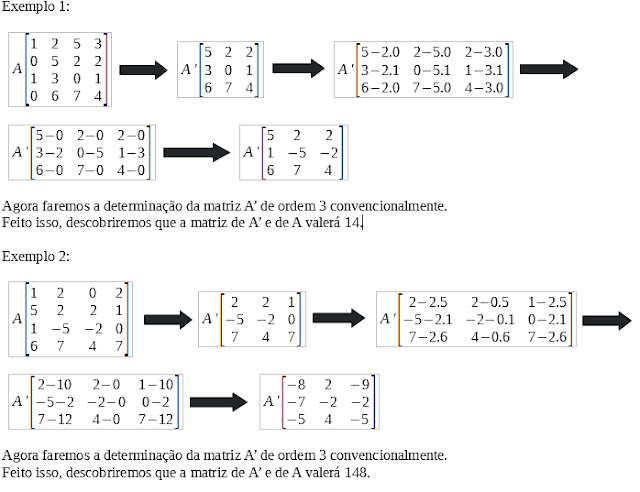
A Regra de Chió nos ajuda a construir uma matriz uma matriz com determinante igual a da matriz dada, entretanto, com a ordem menor. Em uma linguagem matemática, a Regra de Chió nos permite calcular o determinante de uma matriz de ordem n atrás de uma matriz de ordem n-1 (uma ordem abaixo).

Importante: existe uma condição essencial para a aplicação da Regra de Chió, o primeiro elemento da matriz, o elemento a11, deve ser igual a 1.

A Regra de Chió é da seguinte forma:

* Suprima a primeira linha e a primeira coluna da matria;

* Dos elementos que restaram da matriz, subtraia o produto dos dois elementos (um da linha e o outro da coluna) correspondente a este elemento restante.

Esse processo pode ser feito até atingir uma matriz de ordem 3, sendo que as matrizes anteriores têm que ter a11 = 1, pode-se aplicar a característica primeiramente exposta para obter o primeiro elemento igual a um.

Exemplos:

A Regra de Chió é útil para resolver equações lineares com quatro incógnitas, por meio da Regra de Cramer, a qual utiliza os valores das determinantes de matrizes.